【欧拉函数】
任务开始。
- 什么是欧拉函数?我们又怎么求呢???
- 此次任务的主要怪物:欧拉函数
(1)欧拉函数定义
欧拉函数嘛,当然是我们著名的莱昂哈德·欧拉发明的啦~那么他是怎么定义介个函数滴?
咳咳,对正整数n,欧拉函数是小于n的正整数中与n互质的数的数目(φ(1)=1)
啊?这就完了?好像挺简单的啊。。。
但是不要小瞧他,看过的各位可能还记得这样一张图:

当时是不是对它一知半解有点懵?现在我们来认真的导一下,彻底学习~
(2)欧拉函数性质
1.φ(n)=n-1 当且仅当n为质数
这这这,这不废话吗,n要是质数的话小于n的数里面不都跟它互质吗!过过过过过
2.φ(pa)=pa-pa-1 p为质数
em...这个稍微有点意思了。对于pa而言,与它不互质的数必然含有因子p,说白了就是所有p的倍数都不与它互质
而这些数的数量就是(pa)/p=pa-1,然后再一减,就有了这个式子!下一个~!
3.φ(n*m)=φ(n)*φ(m) 当gcd(n,m)=1时
难度逐渐上升了呢,这个证明比较复杂。务必参考
不过我在这里会进一步的解释,你准备好这场惊心动魄的狩猎了吗?
首先我们列个矩阵:
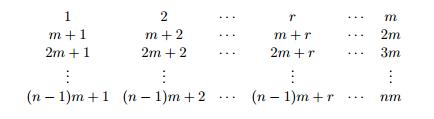
可见这里我们拿出了所有n*m以内的数,每个数都可以表示为k*m+r,其中k为第几行(从0开始),r为第几列(从1开始)
接下来明确我们要求的:phi(n*m)
想要让一个数与n*m互质,只要满足其与n互质,又满足与m互质即可(设gcd(a,n)=1且gcd(a,m)=1。首先因为n与m互质,所以将n与m分别拆分质因数
,你会发现他们没有共同的质因子,而mn的质因子就为他们两个质因子的合集。如果a与n互质,那么他与n没有共同的质因子,同理与m也没有共同的
质因子,所以把a与mn放在一起,你理所应当的发现他们没有共同的质因子,即gcd(a,mn)=1)
所以求解就变成了所有即与n互质又与m互质的数
由于 GCD(km+r, m)=GCD(r, m)(记得辗转相除法吗?),所以每一列的 n 个元素同时与 m 互素当且仅当 GCD(r,m)=1,
因此与 m 互素的列共有phi(m)列。
假定第 r 列元素满足 GCD(r,m)=1. 则该列的所有元素为
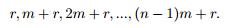
而我们需要验证的是,这些数中有phi(n)个数是与n互质的
首先我们要知道这些数组成了一个mod n的完全剩余系。
什么是完全剩余系呢?就是说有n-1个数,这些数除n的余数两两不相同,就说这些数构成了模n完全剩余系。
怎么证明这一点呢?
设其中的两个数分别为r+am,r+bm(0<=a,b<n),假设a!=b,同时他们除n的余数相同,这就不是完全剩余系。这个条件写为:(r+am)%n==(r+bm)%n
所以[(r+am)%n]-[(r+bm)%n]==0,根据模运算,这么写也可以:
[(r+am)-(r+bm)]%n==0
所以[(a-b)m]%n==0
要想让这个式子成立,只有以下两种可能:
- a-b==0,但是因为a!=b,所以不成立。
- (a-b)m是n的倍数,因为gcd(m,n)=1,所以(a-b)==kn(k>=1),但是因为0<=a,b<n,所以仍然不成立
综上所述,假设不成立,所以这些数构成了模n完全剩余系
根据gcd(r+km,n)==gcd((r+km)%n,n),问题就转化成了[1,n-1]有多少与n互质的数(0肯定不行),没错就是我们一直梦寐以求的phi(n)!
在这mn个数中,有phi(m)列与m互质,这些列中又各自有phi(n)个数与n互质,
综上所述!phi(m*n)=phi(m)*phi(n)!(当且仅当gcd(m,n)=1)
4.φ(n)=n*∏1-1/p 其中p是n的质因子
这一条可以翻译成这样:
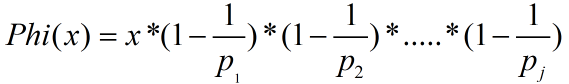 其中p1到pj为x所有的质因子
其中p1到pj为x所有的质因子
证明:拆n->p1a1*p2a2*......*pjaj
用第3条变成:phi(n)=phi(p1a1)*phi(p2a2)*...*phi(pjaj)
再用第2条变成:p1a1*p2a2*...*pjaj*(1-p1-1)*(1-p2-1)*...*(1-pj-1)
化简得证~~
5.φ(2*n)=φ(n) 当n是奇数时
因为n为奇数,所以由 n到2n的变化中增加了质因子”2“,根据第四条可以变成:
φ(2*n)=φ(n)*2*(1-1/2)=φ(n),得证
6.φ(n) mod 2=0 当n>2时
由于第5条,我们只需要证明n为奇数或为2^a(a>1)时成立即可
- n=2^a(a>1),所以phi(n)=2a-2a-1=2a-1*(2-1)为偶数
- n为奇数,则n拆分后必有奇质因数,而pa与pa-1都为奇数,所以pa-pa-1必为偶数
综上,得证
(哎我去切了半天刀都钝了了TAT赶快磨下)

【砥石】入手!
有了这些素材性质做武器工具,我们就能更好的讨伐欧拉函数啦!让我们进入正题吧!
(3)欧拉函数计算
算法1:
这个线性筛你们一定眼熟,不眼熟赶快去看!在这里不讲了
时间代价:O(n)
缺点:处理大范围数据是比较憋手
优点:能求出范围内所有的欧拉函数值还附赠素数表~~
算法2:公式拆

这个算法是基于欧拉函数的第4条性质的,就是将n分解质因数,从而求出他的欧拉函数值。看看吧:
int euler(int n){ //返回euler(n) int res=n,a=n; for(int i=2;i*i<=a;i++){ if(a%i==0){ res=res/i*(i-1);//先进行除法是为了防止中间数据的溢出 while(a%i==0) a/=i; } } if(a>1) res=res/a*(a-1); return res; }
其中注意,a是一个专门用来分解质因数的变量,res储存的是phi的值,结合定义理解下哈~
时间代价:O(√n)
缺点:算了半天只能求一个值
优点:良好的时间代价让她应付起大数据得心应手
(4)欧拉定理
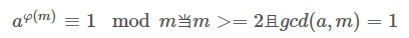
本人才疏学浅,在这里无法给予详细的证明,只知道,这个定理可以用来求逆元。但今后必将补上这个空缺,尽情期待。。。
(5)欧拉函数习题讨伐
1.HSDFZ2436
2.HSDFZ4269
3.HSDFZ4270
三道裸题,灵活应用两种方法即可讨伐成功(但注意第二题longlong,第三题推荐快读)
4.HSDFZ1308/BZOJ2190/SDOI2008
这道题要巧妙的找到问题与“互质”的转化,做到这一点就可以轻松解决了~
首先我们要考虑什么情况下,一个同学无法被看见?当然是他被另一个同学挡住了啦!这个时候满足什么条件呢?没错!设被挡的为(k*x,k*y)
那么(x,y)一定能挡住他!所以当坐标的两个数gcd(x,y)=1时,他才能被看见!而此时x,y互质!!
找到这条性质后问题就迎刃而解了~
5.HSDFZ4688/bzoj2818
如何转化呢?如果x,y互质,p为素数,那么(xp,yp)和(yp,xp)一定是满足条件的数对(因为他们显而易见的只有p为公因数)
知道这个条件后问题就转化了,我们可以规定数对(x,y)中x>y,那么这样的数对个数即phi(x),
只要对于每个x,ans+=phi(x)*2*cnt,其中cnt为质数的个数,这些素数必须满足x*p<n
最后再加上所有的(x,x):ans+=cnt,这里cnt为所有的素数(n以内)
以上的思路虽然可以,但是实现的时候会发现一些细节导致会超时,解决方法提示:不枚举x,枚举素数
6.HSDFZ1356
首先我们知道n!肯定是m!的倍数(废话),接下来考虑一件事:
如果数p(p<=m!)与n!互质,那么gcd(p+k*m!,n!)也必然得1。所以答案理所应当表示成这样:phi(m!)*n!/m!
然后还可以写成:m!*Π(p-1)/p*n!/m!,其中p一目了然就是m以内的所有质数,最后是这样:n!*Π(p-1)/p
预处理n!和一定范围内Π(p-1)/p的总和就好了~~这样针对每个T都可以O(1)出解,不过要用到一些逆元的知识,这里我们以后再说吧。
如果R不是素数这道题依然可做!——中国剩余定理!
(6)结语
事实上,欧拉函数仍然只是数论的基础知识,在许多题目都会看到他的身影。希望今后各位能勇往直前,让今天的学习成为数论领域上的一把利剑!
那么最后。。。

获得部位破坏奖励:素材【phi(m*n)=phi(m)*phi(n)】入手!
end————————2018/3/9
